选择排序

1 简单选择排序

简单选择排序法 (Simpple Selection Sort) 就是通过 n - i 次关键字间的比较，从 n- i + 1 个记录中选出关键字最小的记录，并和第 i ( 1 <= i <= n) 个记录交换之。

思路：遍历第i到第n个，找到i到n范围内最小的数，然后放在i的位置。接着遍历i+1到第n个，找到i+1到n范围内最小的数，然后放在i+1的位置，重复执行下去，最后数组从小到大排列。

public static void selectSort(int array[]){
    for (int i = 0; i < array.length; i++) {
        int min=array[i];
        int index=i;
        for (int j = i; j < array.length; j++) {
            if(array[j]<min)
            {
                min=array[j];
                index=j;
            }
        }
        swap(array,index,i);
    }
}

复杂度分析

O(n²)，性能上略优于同为O(n²)的冒泡排序

2 堆排序

堆是具有下列性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆; 或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆

堆排序 (Heap Sort) 就是利用堆进行排序的方法。

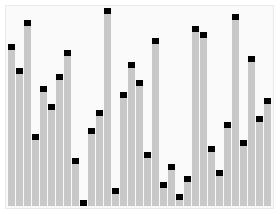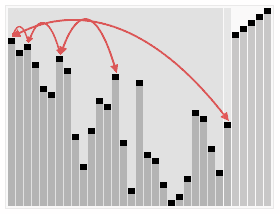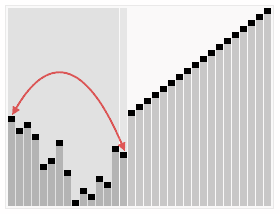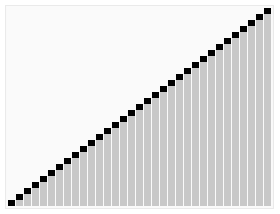
思路：将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根结点。将官移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的 n - 1 个序列重新构造成一个堆，这样就刽寻到 n 个元素中的次小值。如此反复执行， 便能得到一个有序序列了。

public static void heapSort(int array[]){
    int j=array.length;
    //构建堆
    for (int i = j/2-1; i >=0; i--) {
        f(i,j,array);
    }
    //堆排序，从后面的节点开始更第一个节点交换位置，然后进行调整，这样数组将从大到小排列
    for (int i = j-1; i>=0; i--) {
        swap(array,i,0);
        f(0,i,array);
    }
}

public static void f(int low,int high,int array[]){
    int i=low;
    int j=2*i+1;
    int temp=array[i];
    while(j<high){
        //左节点和有节点哪个大
        if(j<high-1&&array[j]>array[j+1]){
            j++;
        }
        //如果大于根节点，进行上浮，将该节点上浮，对下面的子树再进行调整
        if(array[j]<temp){
            array[i]=array[j];
            i=j;
            j=2*i+1;
        }else{
            break;
        }
    }
    array[i]=temp;
}

复杂度分析

O(n*logn)。远远好过于冒泡、简单选择、 直接插入的 O(n²)

由于初始构建堆所需的比较次数较多，因此并不适合待排序序列个数较少的情况