一、二分查找和AVL树查找
二分查找要求元素可以随机访问,所以决定了需要把元素存储在连续内存。这样查找确实很快,但是插入和删除元素的时候,为了保证元素的有序性,就需要大量的移动元素了。
如果需要的是一个能够进行二分查找,又能快速添加和删除元素的数据结构,首先就是二叉查找树,二叉查找树在最坏情况下可能变成一个链表,于是就出现了平衡二叉树,根据平衡的算法不同有AVL树,B-Tree,B+Tree,红黑树等。
但是AVL树实现起来比较复杂,平衡操作较难理解,这时候就可以用SkipList跳跃表结构。
二、什么是跳跃表
Skip list 是一种可以代替平衡树的数据结构,默认是按照 Key 值升序的。Skip list 让已排序的数据分布在多层链表中,以 0-1 随机数决定一个数据的向上攀升与否,通过“空间来换取时间”的一个算法,在每个节点中增加了向前的指针,在插入、删除、查找时可以忽略一些不可能涉及到的结点,从而提高了效率。
在Java的API中已经有了实现:
- ConcurrentSkipListMap:在功能上对应 HashTable、HashMap、TreeMap
- ConcurrentSkipListSet:在功能上对应 HashSet
跳跃表以有序的方式在层次化的链表中保存元素, 效率和AVL树媲美 —— 查找、删除、添加等操作都可以在O(LogN)时间下完成, 并且比起二叉搜索树来说, 跳跃表的实现要简单直观得多。
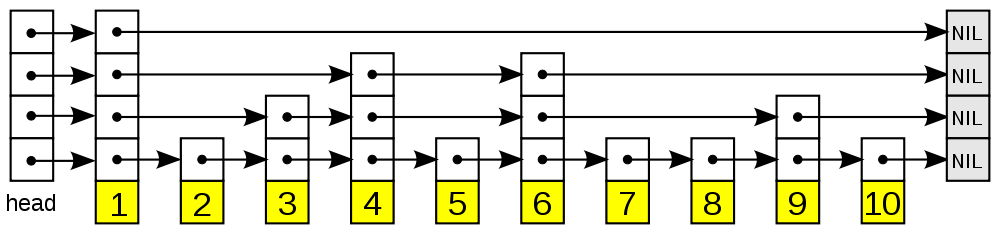
从图中可以看到, 跳跃表主要由以下部分构成:
- 表头(head):负责维护跳跃表的节点指针。
- 跳跃表节点:保存着元素值,以及多个层。
- 层:保存着指向其他元素的指针。高层的指针越过的元素数量大于等于低层的指针,为了提高查找的效率,程序总是从高层先开始访问,然后随着元素值范围的缩小,慢慢降低层次。
- 表尾:全部由 NULL 组成,表示跳跃表的末尾。
三、跳跃表的构造
一个跳表,应该具有以下特征:
- 一个跳表应该有几个层(level)组成;
- 跳表的第一层包含所有的元素;
- 每一层都是一个有序的链表;
- 如果元素x出现在第i层,则所有比i小的层都包含x;
- 第i层的元素通过一个down指针指向下一层拥有相同值的元素;
- 在每一层中,-1和1两个元素都出现(分别表示INT_MIN和INT_MAX);
- Top指针指向最高层的第一个元素。
实例

构造一个3层的跳跃表
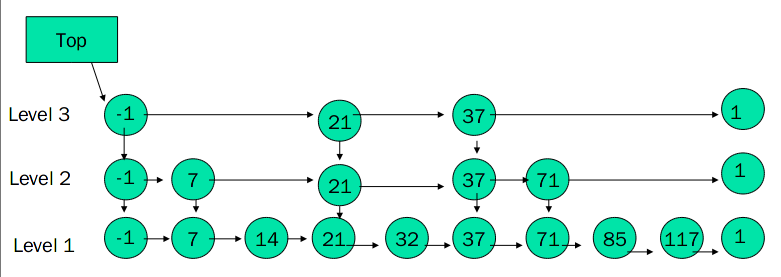
Skip List构造步骤:
- 给定一个有序的链表。
- 选择连表中最大和最小的元素,然后从其他元素中按照一定算法(随机)随即选出一些元素,将这些元素组成有序链表。这个新的链表称为一层,原链表称为其下一层。
- 为刚选出的每个元素添加一个指针域,这个指针指向下一层中值同自己相等的元素。Top指针指向该层首元素
- 重复2、3步,直到不再能选择出除最大最小元素以外的元素。
四、操作
1)查找
查找19是否存在。从头结点开始,首先和9进行判断,此时大于9,然后和21进行判断,小于21,此时这个值肯定在9结点和21结点之间,此时,和17进行判断,大于17,然后和21进行判断,小于21,此时肯定在17结点和21结点之间,此时和19进行判断,找到了:

2)插入
插入包含如下几个操作:
1、查找到需要插入的位置
2、申请新的结点
3、调整指针。
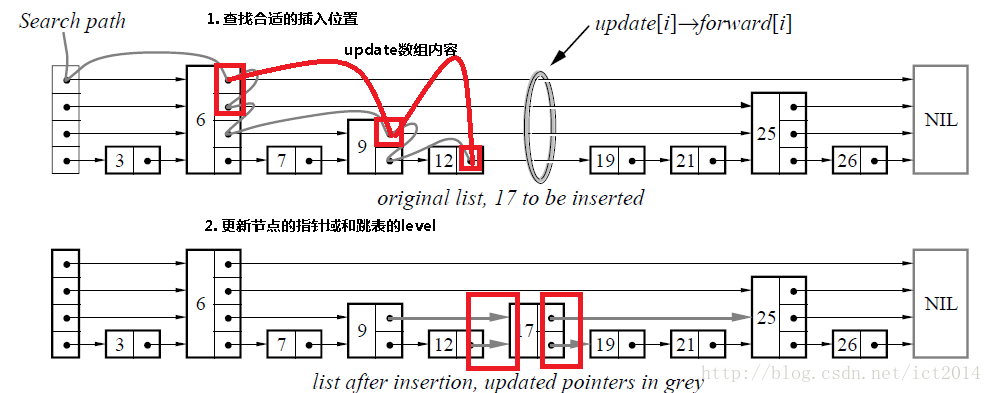
查找如下图的灰色的线所示 申请新的结点如17结点所示, 调整指向新结点17的指针以及17结点指向后续结点的指针。这里有一个小技巧,就是使用update数组保存大于17结点的位置,这样如果插入17结点的话,就指针调整update数组和17结点的指针、17结点和update数组指向的结点的指针。update数组的内容如红线所示,这些位置才是有可能更新指针的位置。
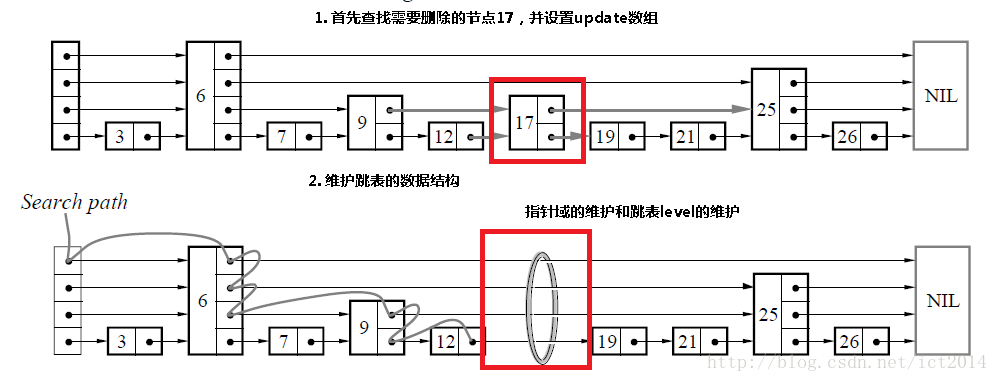
3)删除
删除操作类似于插入操作,包含如下3步:
1、查找到需要删除的结点
2、删除结点
3、调整指针
参考
浅析SkipList跳跃表原理及代码实现 https://blog.csdn.net/ict2014/article/details/17394259
跳跃表Skip List的原理和实现 https://yq.aliyun.com/articles/38381