1 数组的概念、多维数组的实现
1)数组的概念
- 数组的特点:元素数目固定;下标有界。
- 数组的操作:按照下标进行读写。
2)多维数组的实现
行优先顺序
存储时先按行从小到大的顺序存储,在每一行中按列号从小到大存储。
列优先顺序
存储时先按列从小到大的顺序存储,在每一列中按行号从小到大存储。
2 矩阵的压缩存储
矩阵的压缩存储就是存储数组时,尽量减少存储空间,但数组中每个元素必须存储。
在矩阵中,如果有规律可寻,只要存储其中一部分,而另外一部分的存储地址可以通过相应的算法将它计算出来,从而占有较少的存储空间达到存储整个矩阵的目的。
矩阵的压缩存储仅能针对特殊矩阵使用,对于没有规律可循的二维数组则不能使用。
1)对称矩阵
只需对对称矩阵中n(n+1)/2个元素进行储存表示
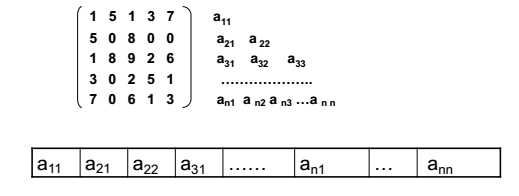
2)三角矩阵
以主对角线划分,三角矩阵有上三角和下三角两种。上三角矩阵它的下三角中的元素均为常数。下三角矩阵正好相反,它的主对角线上方均为常数。

3)稀疏矩阵
if 一个 m * n 的矩阵含有 t 个非零元素,且 t 远远小于 m * n,则称这个矩阵为稀疏矩阵

除了记录非零元素的值之外,还必须同时几下它所在的行和列的位置。稀疏矩阵的存储方法一般有三种:三元组法、行逻辑连接顺序表和十字链表法。
三元组法
用三项内容表示稀疏矩阵中的每个非零元素,形式为:(i,j,value)。
其中,i 表示行序号,j 表示列序号,value 表示非零元素的值
3 广义表的基本概念
1)定义
- 广义表:是线性表的扩展,具体定义为n(n≥0)个元素的有限集合。
n的值是广义表的长度,如果n=0称广义表为空表。 - 长度:广义表中含有元素的个数称
- 深度:广义表中含有的括号对数
数据元素
广义表的数据元素有两种类型:一个是不可再分的元素(原子元素);一个是可以再分的元素(子表)。
- 如果所有的元素都是原子元素,则称为线性表。
- 如果数据元素中含有子表元素,则称为广义表。
记法
广义表一般记作:LS=(a1,a2,……,an)
常见的广义表为:A=()、B=(())、C=(a,b)、D=(A,B,C)、E=(a,E)
特点
广义表有三个重要的特点:
- 第一:广义表的元素可以是子表,而子表的元素还可以是子表,广义表是一个多层次的结构。
- 第二:广义表可以为其他广义表所共享。
- 第三:广义表可以是一个递归表,即表也可以是其本身的一个子表。
2)存储方式
广义表的存储方法有很多种,一般采用链表存储。

flag表示标志位。当flag为0时,表示该结点为原子元素,info表示原子元素的值;当flag为1时表示该结点为子表,info表示指针,指向该子表的第一个结点。 link表示指针,指向广义表的下一个元素。