数据的表示和运算

Wu Jun 2020-03-16 18:57:23

Categories： Tags：

1 数制与编码

1.1 进位计数制及其相互转换

1）进位计数制

进位计数法是一种计数的方法，生活中常用 10 进制数表示，计算机内常用二进制、八进制、十六进制表示数据。

二进制
- 计算机中使用最多的是二进制数，二进制数只有两个数字符号 0/1，计数逢二进一，任意位的权重位 2ⁱ，i 为所在位数。
八进制
- 八进制是二进制的一种书写形式，基数为 8，逢 8 进 1。因为 8=2³，所以只要把二进制 3 位编码成一组就是 1 位八进制数。
十六进制
- 十六进制数是用 0~9 A~F 这 16 个符号来表示的，因为 16=2⁴，所以每 4 位二进制数分为一组，便可表示一位十六进制数。

2）不同进制之间的相互转换

二进制 -> 八进制/十六进制
- 对于一个含小数部分的二进制数，在转换时要以小数点为界。
- 整数部分：从右往左，每 3 位（八进制）或 4 位（十六进制）一组，最左边用 0 补成满 3 位（八进制）或 4 位（十六进制）
- 小数部分：从左往右，每 3 位（八进制）或 4 位（十六进制）一组，最右边可能要用0补满 3 位（八进制）或 4 位（十六进制）
- 然后整数、小数部分分别用对应的八进制（十六进制）数代替 3 位（4 位）二进制数即可。
八进制/十六进制 -> 二进制
- 只需将每一位改为 3 位或 4 位二进制数即可，必要时去掉整数最高位或小数最低位的 0
八进制 <-> 十六进制
- 先转为二进制，再由二进制转换
任意进制 - > 十进制
- 按权展开相加法：任意进制数到十进制的转换都可以把它们各位数值与权值相乘，再把所有乘积相加。
十进制 -> 任意进制
- 十进制到任意进制的转换采用基数乘除法。
- 整数部分（除基取余法）：整数部分除基取余，最先得到的余数为结果的最低位，最后取得的余数为最高位，商为0时结束。（除基余取，先余为低，后余为高）
- 小数部分（乘基取整法）：小数部分乘基取整，最先得到的整数位结果的最高位，最后取得的整数位最低位，乘积为0（或满足精度要求）时结束。（乘积取整，先整为高，后整为低）
- 最后将两部分拼接起来。

例：将十进制数 123.6875 换为二进制。

计算机整数是连续表示的，但是小数是离散的，所以并不是每个十进制小数都可以准确地用二进制表示，例如 0.3，但是任何一个二进制小数都可以用十进制小数表示

1.2 真值和机器数

1）真值

真值就是我们日常用到的用正负号表示正负数的数（正号可省略），比如 +4、-1 等。真值是机器数要表示的实际值。

2）机器数

机器数是真值在计算机中表示的表示形式，是符号数值化的带符号二进制数。

机器数的特点是：表示的数值范围受计算机字长限制；机器数的符号位必须被数值化为0和1；机器数的小数点是用规定的隐含方式来表达的。

1.3 BCD 码

BCD 码是 Binary-Coded Decimal（二进制编码的十进制数）的简称，通常用 4 位二进制数表示 1 位十进制数。

这种编码方式，使十进制和二进制之间转换得以快速进行。但 4 位二进制有 16 种组合，必然会有 6 个冗余。

1）8421 码

有权码，4 位二进制数各位的权值分别是 8、4、2、1。
- 如 0111 表示的是 0 * 8 + 1 * 4 + 1 * 2 + 1 * 1 = 7 这个十进制数。
如果 8421 码运算后大于（1001）₂，则要加 6，即（0110）₂，修正，并向上进位。
- 如计算 8 + 4 = 12 时：1000 + 0100 = 1100 > 1001 ==> 1100 + 0110 = 10010 = 12

2）余 3 码

无权码，在 8421 码的基础上，把每个编码都加上 0011
当两个余三码相加，不产生进位时，应从结果中减去 0011；产生进位时，应将进位信号送入高位，本位加 0011

3）2421 码

有权码，各位权重分别为 2、4、2、1
特点是大于等于 5 的四位二进制树中最高位为 1，小于 5 的最高位为 0

4）格雷码

无权码，任何两个相邻编码只有 1 个二进制位不同，而其余 3 个二进制位相同

5）5211 码

有权码，各位权重分别为 5、2、1、1
5211 码的每一位正好与 8421 码十进制计数器 4 个触发器输出脉冲的分频比相对应

1.4 字符与字符串

由于计算机只能处理二进制数据，所以所有字符都要编码成二进制来表示。

1）字符编码 ASCII 码

ASCII 码是用 7 位二进制数表示一个字符的系统。

其中编码值 0～31 是控制字符，编码值 127 是 DEL 码，编码值 32 是空格，编码值 32～126 共 95 个是可印刷字符。

为什么 0~9 对应 ASCII 码 48~57？因为 48 二进制形式为 0110000 ，去掉高三位即 0，其他数字亦然

2）汉字的表示和编码

汉字的编码包括汉字的输入编码、汉字内码、汉字字形码三种，分别用于输入、内部处理和输出三种用途。

区位码
- 区位码是用两个字节表示一个汉字，每个字节用 7 位，把所有汉字表示在一个 94 * 94 的二维表格中，每一行称为一个区，每一列为一个位
- 区位码是用 4 位十进制数表示某个汉字的，前两位是区码，后两位是位码
国标码
- 为了与 ASCII 码兼容，国标码是把十进制区位码转换成十六进制后，每个字节加 20H
- 国标码 = （区位码）₁₆ + 2020H（2020H 即 00100000 00100000）。
汉字内码
- ASCII 码最高位是 0，为了方便计算机区分中文字符和英文字符，将国标码两个字节的最高位均设置为 1，即为汉字内码。
- 汉字内码 = （国标码）₁₆ + 8080H（8080 即 1000000 1000000）。

3）字符串的存放

字符串是指连续的一串字符，通常占用主存中连续的多个字节，每个字节存储一个字符。

需要区分“大端模式”和“小端模式”

大端模式（低位优先）：数据的高字节保存在内存的低地址中，而数据的低字节保存在内存的高地址中；地址由小向大增加，而数据从高位往低位放。
小端模式（高位优先）：数据的高字节保存在内存的高地址中，而数据的低字节保存在内存的低地址中，和我们的逻辑方法一致。

例如 16 位值 0x2122

大端模式：0x22 0x21
小端模式：0x21 0x22

不同计算机可以选用任何一种，甚至同时采用

x86 和一般的 OS（如windows，FreeBSD,Linux）使用的是小端模式。
Mac OS 是大端模式。

1.5 校验码

校验码：校验码是指能够发现或自动纠正错误的数据编码
- 校验码的实现原理是添加一些冗余码，来检验或纠错。
码距：数据校验码的码距是指任何两个合法码字之间最少变化的二进制位数
- 对于码距不小于 2 的数据校验码，开始具有检错能力，且码距越大，检错、纠错能力越强，检错能力总是大于等于纠错能力

1）奇偶校验码

在原编码基础上添加一个校验位，码距为 2，可以检测出一位错误（或奇数位错误），但不能找到出错位置，也不能检测偶数位错误。增加的冗余位称为奇偶校验位。

奇校验码：添加一位后，整个编码中有奇数个 1。
偶校验码：添加一位后，整个编码中有偶数个 1。

2）海明（汉明）校验码

是一种多重奇偶校验码。原理是在有效信息中加入几个校验位形成海明码，并把海明码的每一个二进制位分配到几个奇偶校验组中。当某一位出错后，就会引起有关的几个校验位的值发生变化，所以不但可以发现错位，还能纠正错位。

根据纠错理论得 L - 1 = D + C (D>=C)，即编码最小码距 L 越大，其检错位 D 数就越大，纠正错误的位数 C 也越大，并且纠错能力恒小于或等于检错能力。

例，在 n = 4，k = 3 时，求 1010 的汉明码

确定海明码的位数
- 设有 n 位有效信息的位数，k 为校验位的位数，则信息位 n 和校验位 k 应满足：n + k <= 2² - 1。海明码位数为 n + k = 7 <= 2³ - 1 成立，则 n、k 有效。设信息位 D₄D₃D₂D₁(1010)，共 4 位，校验码 P₃P₂P₁，共三位，对应的海明码为 H₇H₆H₅H₄H₃H₂H₁。
确定校验位的分布
- 规定校验位P_i在海明位号为2_i-1的位置上，其余各位为信息位，因此：
  - P₁的海明位号为2^i-1 = 2⁰ = 1，即H₁为P₁。
  - P₂的海明位号为2^i-1 = 2¹ = 2，即H₂为P₂。
  - P₃的海明位号为2^i-1 = 2² = 4，即H₄为P₃。
- 将信息位按原来的顺序插入，则海明码各位分布如下：
  
  H₇ H₆ H₅ H₄ H₃ H₂ H₁
  
  D₄ D₃ D₂ P₃ D₁ P₂ P₁
分组，以形成校验关系
- 每个数据位用多个校验位进行校验，但要满足：被校验的数据位的海明码位于等于校验该数据位的各校验位海明位号之和。另外，校验位不需要再被校验。
  - D₁ 在 H₃ 的位置，所以由 P₂P₁ 校验
  - D₂ 在 H₅ 的位置，所以由 P₃P₁ 校验
  - D₃ 在 H₆ 的位置，所以由 P₃P₂ 校验
  - D₄ 在 H₇ 的位置，所以由 P₃P₂P₁ 校验
校验位取值
- 校验位 P_i 的值分为 i 组（由该校验位校验的数据位）所有位求异或。根据 3 的分组，有：
  - P₁ = D₁⊕D₂⊕D₄ = 0⊕1⊕1 = 0
  - P₂ = D₁⊕D₃⊕D₄ = 0⊕0⊕1 = 1
  - P₃ = D₂⊕D₃⊕D₄ = 1⊕0⊕1 = 0
- 所以 1010 对应的海明码为 1010010
海明码校验的原理
- 每个校验组分别利用校验位和参与形成该校验位的信息位进行奇偶校验检查，就构成了 k 个校验方程：
  - S₁ = P₁⊕D₁⊕D₂⊕D₄
  - S₂ = P₂⊕D₁⊕D₃⊕D₄
  - S₃ = P₃⊕D₂⊕D₃⊕D₄
- 若 S₃S₂S₁ 的值为“000”，则说明无错，否则说明出错，而这个数就是错误的位号。

H₇	H₆	H₅	H₄	H₃	H₂	H₁
D₄	D₃	D₂	P₃	D₁	P₂	P₁

3）循环冗余校验（CRC）码

CRC 的基本思想是：在 K 位信息码后再拼接 R 位的校验码，整个编码长度为 N 位，因此这种编码又称为（N, K）码。
CRC 码基于线性编码理论，在发送端，将要传送的 K 位二进制信息码左移 R 位，将它与生成多项式 G(x) 做模 2 的除法，生成一个 R 位校验码，并附在信息码后，构成一个新的二进制码（CRC 码），共 K+R 位。在接收端，则利用生成多项式对接收到的编码做模 2 的除法，以检测和确定出错的位置，若无错则整除，生成多项式是接收端和发送端的一个约定。
任意一个二进制数码都可以用一个系数仅为 0 或 1 的多项式与其对应。生成多项式 G(x) 的最高幂次为 R，转换成对应的 2 进制数有 R+1 位。例如多项式 x³+x²+1 对应的二进制数为 1101。

例，设生成多项式为 G(x) = x³+x²+1，信息码为 101001 ，求对应的 CRC 码：

R = 生成多项式最高幂次 = 3，K = 信息码长度 = 6， N = K + R = 9

移位
- 将原信息码左移R位，低位补 0，得 101001000
相除
- 对移位后的信息码，用生成多项式进行模2除法，产生余数。得到余数为 001，则 101001 编码后的 CRC 码为 101001001。
检错和纠错
- 接收到 CRC 码，用生成多项式 G(x) 做模 2 的除法，若余数为 0，则码字无错。
- 若接收端接收的 CRC 码为 101001011，将这个数据与 1101 进行模 2 除法，得到余数 010，则说明倒数第二位出粗，将其取反即可。

模2除法：

模 2 加法和减法的结果相同，都是做异或运算，模 2 除法和算术除法类似，但每一位除（减）的结果不影响其他位，也就是不进位，过程如下：

用除数对被除数最高几位做模 2 减（异或，不借位）

除数右移 1 位，若余数做高位为 1，商为 1，并对余数做模 2 减。若余数最高位为 0，商为 0，除数继续右移一位。

循环直到余数位数小于除数时，该余数为最终余数。

2 定点数的表示和运算

2.1 定点数的表示

1）无符号数和有符号数的表示

无符号数：整个机器字长的全部二进制位都是数值位，没有符号位，相当于数的绝对值，若机器字长为 8，则无符号数的表示范围是 0～2⁸-1，即 0～255。
有符号数：在机器中，数的正负是无法直接表示的，所以一般用符号 0 表示正，用符号 1 表示负，从而将正负数值化。

2）机器数的定点表示

根据小数点的位置是否固定，计算机中机器数分两种数据格式：定点表示和浮点表示。

定点表示法约定所有机器数的小数点位置固定不变，可以分为定点整数、定点小数两种。

定点小数（纯小数）：小数点隐含在符号位之后、有效数值位之前
定点整数（纯整数）：小数点隐含在有效数值为之后

3）原码、反码、补码、移码

原码
- 定义：用机器数的最高位作为符号位，正为 0，负为 1，其余各位表示数的绝对值。
- 特点：
  - 原码的 0 有两种表示方法：00000，10000。正负两部分相互独立，只要越界就溢出了
  - 正数的原码码值随着真值增长而增长，负数的原码码值随着真值增长而减少
  - n+1 位原码表示定点整数范围 -(2ⁿ-1) ~ 2ⁿ-1，n+1 位原码表示定点小数范围 -(1-2^-n) ~ 1-2^-n
反码
- 当要表示的数为正数时反码和原码相同，是负数时除符号位外其他位都取反
- 例如 +1101，-1101，+0.1010，-0.1010 的反码分别表示为 01101，10010，0.1010，1.0101。
补码
- 补码是最重要的一种编码方式。编码方式是在原码的基础上，若是正数，和原码完全一样，若是负数，则原码除符号位外其他位取反再加 1
- 例如 +1101，-1101，+0.1010，-0.1010 的补码分别表示为 01101，10011，0.1010，1.0110。
- 补码运算的技巧
  - 对补码进行补码运算可得原码
  - 对补码进行带上符号位的补码运算可得其相反数的补码
移码
- 移码只能表示整数，常用来表示浮点数的阶码。
- 和其他机器数表示不同的是它用 1 表示正，用 0 表示负，数值部分和补码相同。
- 将负数域与正数域调换一下（加个偏移量即可），保持了数据原有的大小顺序，移码大真值就大，移码小真值就小

如未特殊说明，各种转换都不带符号位，保证符号位不变

2.2 定点数的运算

1）定点数的移位运算

算术移位：针对有符号数，移位过程中保持符号位不变
- 正数：移位后出现的空位均以 0 填补
- 负数：移位后出现的空位填补方式如下
  - 原码：添补 0
  - 补码：左移添 0，右移添 1
  - 反码：添补 1
逻辑移位：针对无符号数，添补 0
循环移位：适合将数据的低字节部分与高字节部分互换
- 大循环：带进位标志位 CF 的循环移位
- 小循环：不带进位标志位的循环移位

2）原码定点数的加/减运算

加法规则：先判符号位，若相同，绝对值相加，结果符号位不变；若不同，则做减法，绝对值大的数减去绝对值小的数，结果符号位与绝对们大的数相同。
减法规则：两个原码表示的数相减，首先将减数符号取反，然后将被减数与符号取反后的减数按原码加法进行运算。

注意：运算时注仓机器字长，当左边位出现溢出时，将溢出位丢掉。

3）补码定点数的加/减运算

补码加减运算规则简单，易于实现，因此计算机系统中普遍采用补码加减运算。

参与运算的两个操作数均是补码形式
按 2 进制运算规则，逢二进一
符号位与数值位按同样规则参与运算，符号位运算产生的进位要丢掉，结果的符号位由运算得出。
补码的加减法运算依据下面公式进行。当参与运算的数是定点小数时，模 M=2；当参与运算的是定点整数时，模 M=2ⁿ⁺¹。
- [A + B]_补 = [A]_补 + [B]_补 (mod M)
- [A - B]_补 = [A]_补 + [-B]_补 (mod M)
补码运算结果仍为补码

4）符号扩展

在计算机算术运算中，有时必须将采用给定位数表示的数转换成具有不同位数的某种表示形式。

符号位不变

正数：用 0 填充
负数：根据机器数的不同而不同
- 原码：用 0 填充
- 补码：整数用 1，小数用 0 填充
- 反码：用 1 填充

5）溢出概念和判别方法

仅当两个符号相同的数相加，或两个符号相异的数相减才可能产生溢出。

（1）一位符号位判溢出

由于减法在机器中是用加法器实现的，因此无论是加法还是减法，只要参与操作的两个数符号相同，结构与原操作数符号不同，则肯定发生了溢出。

（2）采用双符号位

双符号位法也称模 4 补码，额外增加一位符号位。运算结果的两个符号位 S₁S₂ 相同，表示未溢出，不同，表示溢出，此时最高位代表真正的符号。

符号位 S₁S₂ 的各种情况如下：

S₁S₂ = 00：表示结果为正，无溢出
S₁S₂ = 01：表示结果正溢出
S₁S₂ = 10：表示结果负溢出
S₁S₂ = 11：表示结果为负，无溢出

则溢出逻辑判断表达式为 V = S₁⊕S₂，若 V = 0，表示无溢出，V = 1，表示结果溢出。

（3）采用一位符号位根据数据位的进位情况判断

如果符号位的进位 C_s 与最高位的进位 C₁ 相同，则说明没有溢出，否则发生了溢出。则溢出的逻辑判断表达式为 V = C_s⊕C₁，若 V = 0，表示无溢出；V = 1，表示有溢出。

6）定点数的乘法运算

在计算机中，乘法运算由累加和右移操作实现。根据机器数的不同，可分为原码一位乘法和补码一位乘法。原码一位乘法的规则比补码一位乘法简单。

（1）原码一位乘法

两个原码数相乘，其乘积的符号为相乘两数符号的异或值，数值则为两数绝对值之积

设[X]_原＝x_s.x₁x₂…x_n, [YJ_原＝y_s.y₁y₂…y_n，则运算规则如下。

被乘数和乘数均取绝对值参加运算，符号位为 x_s⊕y_s。
部分积的长度同被乘数，取 n+1 位，以便存放乘法过程中绝对值大于或等于 1 的值，初值为 0。
从乘数的最低位 y_n 开始判断：若 y_n=1，则部分积加上被乘数 |x|，然后右移一位；若 y_n=0，则部分积加上 0, 然后右移一位。
重复上一步，判断 n 次。

（2）补码一位乘法（Booth 算法）

它是一种带符号数的乘法，采用相加和相减的操作，计算补码数据的乘积。

设[X]_补＝x_s.x₁x₂…x_n, [YJ_补＝y_s.y₁y₂…y_n，则运算规则如下。

符号位参与运算，运算的数均以补码表示
被乘数一般取双符号位参与运算，部分积取双符号位，初值为 0,乘数可取单符号位。
乘数末位增加附加位 y_n+1 ，且初值为 0
根据（y_n, y_n+1) 的取值来确定操作（如下表）
移位按补码右移规则进行。
按照上述算法进行 n+1 步操作，但第 n+1 步不再移位（共进行 n+1 次累加和 n 次右移），仅根据 y_n 与 y_n+1 的比较结果做相应的运算即可。

y_n（高位）	y_n+1（低位）	操作
0	0	部分积右移一位
0	1	部分积加 [X]_补，右移一位
1	0	部分积加 [-X]_补$，右移一位
1	1	部分积右移一位

7）定点数的除法运算

在计算机中，除法运算可转换成“累加——左移＂（逻辑左移），根据机器数的不同，可分为原码除法和补码除法。

（1）原码除法运算（不恢复余数法）

同原码乘法，需要将符号位与数值部分分开计算

恢复余数法
- 当余数为负时，都需要再加上除数将余数恢复为正值，这将大大增加除法时间，所以一般不用
加减交替法
- 余数为正数时，下一步就直接减就好了
- 余数为负数时，商上 0，在下一步加除数（替换下一步的减，当前步无需额外操作）即可，不需要再额外增加恢复余数这一步了

（2）补码除法运算

和补码乘法一样，不需要单独算符号位

恢复余数法（一般不用，略）
加减交替法
- 若余数与除数同号，则代表上一次够减，商上 1，下一次做减法
- 若余数与除数异号，则代表上一次不够减，商上 0，下一次做加法
- 末位恒置 1

2.3 强制类型转换

同等字长不同类型的变量转换（比如 short 与 unsigned short），将会保留存储时的位值（补码），按照新的类型重新解释
大字长变量向小字长变量转换时（比如 int 向 short），将会将大字长变量高字节部分直接截断
小字长变量向大字长变量转换时（比如 short 向 int），不仅将低字节部分复制过去，而且要对符号位进行扩展补充，以保证数值是不变的

3 浮点数的表示和运算

3.1 浮点数的表示

1）浮点数的表示格式

浮点数由阶码和尾数两部分组成，表示为 N = r^E * M。式中，r 是浮点数阶码的底（隐含），与尾数的基数相同，通常 r=2。E 和 M 都是带符号的定点数，E 称为阶码，M 称为尾数。

2）规格化浮点数

为了提高运算的精度，需要充分地利用尾数的有效数位，通常采取浮点数规格化形式，即规定尾数的最高数位必须是一个有效值。

规格化方法
- 左规：即经过运算后不满足规格化，需尾数左移，阶码减 1（可能进行多次）
- 右规：尾数溢出（双符号位为01或10)时，尾数右移，阶码加 1

3）浮点数表示范围

上溢：运算结果大于最大正数称为正上溢，小于绝对值最大负数称为负上溢，需进行溢出处理
下溢：运算结果在 0 至最小正数之间称为正下溢，在 0 至绝对值最小负数之间称为负下溢，当做机器零处理

4）IEEE 754 标准

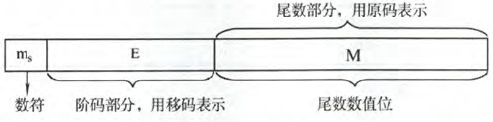
数符：1 位
阶码：移码表示
尾数：原码表示，由于最高位必为 1，为了能够表示更多有效位，这个 1 将隐含

类型	数符	阶码	尾数数值	总位数
短浮点数	1	8	23	32
长浮点数	1	11	52	64
临时浮点数	1	15	64	80

5）定点、浮点表示的区别

范围：浮点范围增加
精度：由于浮点有着很多位表示阶码，所以精度降低
数的运算：浮点运算要对阶码和尾数运算，最后还要规格化，比较复杂
溢出问题：尾数溢出可以右规，阶码溢出才是真的溢出

3.2 浮点数的加减运算

浮点数运算的特点是阶码运算和尾数运算分开进行。浮点数的加／减运算一律采用补码。浮点数加／减运算分为以下几步。

对阶
- 小数点位置对齐，使得两个数的阶码相等。
- 先求阶差，小阶向大阶看齐，将阶码小的尾数右移一位（基数为 2)，阶加 1，直到两个数的阶码相等为止。
- 尾数右移时，舍弃掉有效位会产生误差，影响精度。
尾数求和：将对阶后的尾数按定点数加（减）规则运算
规格化：左规或右规
舍入
- 0 舍 1 入法：类似于十进制的四舍五入
- 恒置 1 法
溢出判断
- 上溢：中断处理
- 下溢：按机器零处理
强制类型转换
- char -> int -> long -> double 范围和精度都从小到大，可以放心转换，不会有损失（溢出或者精度损失）
- 值得注意的是， int -> float 虽然不会发生溢出，但是是可能进行舍入的，因为 float 尾数部分（24bit）比 int 数值（32bit）少，所以最后几位可能会发生舍入

3.3 浮点数的乘除法运算

浮点数阶码运算(移码)
- [X+Y]移=[X]移+[Y]补
- [X–Y]移=[X]移+[–Y]补
按照一位乘或加减交替除运算
- 先确定符号，在列式子计算

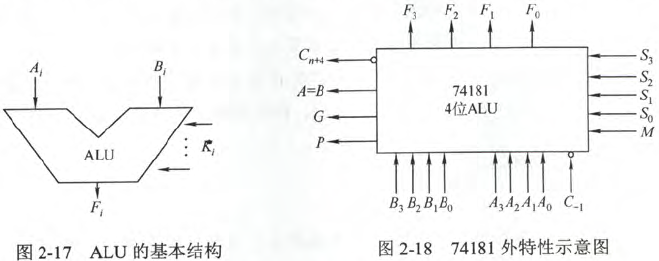
4 算术逻辑单元 ALU

在计算机中，运算器承担了执行各种算术和逻辑运算的工作，运算器由算术逻辑单元 ALU (Arithmetic Logic Unit)、累加器、状态寄存器和通用寄存器组等组成。

ALU 的基本功能包括加、减、乘、除四则运算，与、或、非、异或等逻辑运算，以及移位、求补等操作。

4.1 串行加法器和并行加法器

加法器是由全加器再配以其他必要的逻辑电路组成的，根据组成加法器的全加器个数是单个还是多个，加法器有串行和并行之分。

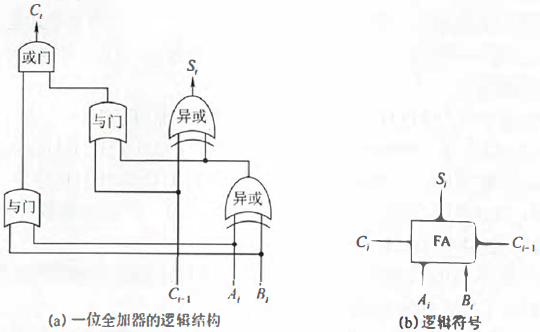
1）一位全加器

全加器（FA）是最基本的加法单元

输入
- 加数 A_i
- 加数 B_i
- 低位进位 C_i-1
输出
- 本位 S_i = A_i⊕B_i⊕C_i-1
- 进位 C_i = A_iB_i + (A_i⊕B_i)C_i-1

2）串行加法器

只有一个全加器，数据逐位送入加法器中进行运算，所以运算慢

3）并行加法器

多个全加器组成，各位同时运算，但是仍有一个制约其速度的最大问题：虽然各位同时提供，但是进位必须在低位计算结束后才能得到

（1）串行进位

正如上面所述，高位仍然需要等待低位的进位，速度仍然受限

（2）并行进位

在高位的表达式中直接带入低位进位的结果，当然这样越高位表达式越复杂，对应的逻辑电路也就越复杂，但这确实解决了速度的问题

分组并行进位方式为了防止电路过于复杂，并获得比较可以接受的速度，可以对全加器进行分组，在组内使用并行进位链，组间需要分情况
- 单级先行进位方式
  - 组内使用并行进位链，组间使用串行进位链
- 多级先行进位方式
  - 相似的，这次使用的是分级的思想，还是需要分组，组内并行进位链，组间也是并行进位链

4.2 算术逻辑单元的功能和结构

ALU 是一种功能较强的组合逻辑电路。它能进行多种算术运算和逻辑运算。由于加、减、乘、除运算最终都能归结为加法运算。因此，ALU 的核心首先应当是一个并行加法器，同时也能执行 “与”、“或”、“非”等逻辑运算。

输入
- 输入变量 A_i，B_i
- 控制信号 K_i ，用于控制做何种运算
输出
- 运算结果 F_i

Spring Cloud Config

计算机系统概述