堆

堆（Heap）是一种特别的树状数据结构：“给定堆中任意节点 P 和 C，若 P 是 C 的母节点，那么 P 的值会小于等于（或大于等于）C 的值”。分为最小堆和最大堆。

1. 二叉堆
2. 左倾堆
3. 斜堆
4. 二项堆
5. 斐波那契堆
6. 索引堆
7. Treap 树堆

1、二叉堆

二叉堆是完全二元树或者是近似完全二元树，按照数据的排列方式可以分为两种：最大堆和最小堆。

二叉堆一般都通过"数组"来实现

2、左倾堆

左倾堆(leftist tree 或 leftist heap)，又被成为左偏树、左偏堆，最左堆等。

它和二叉堆一样，都是优先队列实现方式。可以高效解决"对两个优先队列进行合并"的问题。

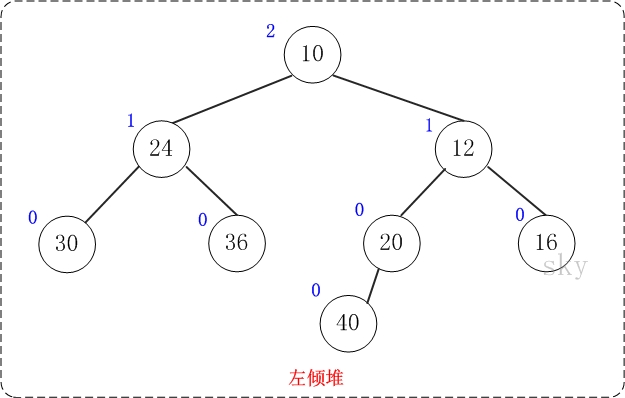
上图是一颗左倾树，它的节点除了和二叉树的节点一样具有左右子树指针外，还有两个属性：键值和零距离。

• 键值：作用是来比较节点的大小，从而对节点进行排序。
• 零距离：是从一个节点到一个"最近的不满节点"的路径长度。不满节点是指该该节点的左右孩子至少有有一个为NULL。叶节点的NPL为0，NULL节点的NPL为-1。

左倾堆有以下几个基本性质：

• 节点的键值小于或等于它的左右子节点的键值。
• 节点的左孩子的NPL >= 右孩子的NPL。
• 节点的NPL = 它的右孩子的NPL + 1。

合并两个左倾堆的基本思想如下：

1. 如果一个空左倾堆与一个非空左倾堆合并，返回非空左倾堆。
2. 如果两个左倾堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将"较小堆的根节点的右孩子"和"较大堆"进行合并。
3. 如果新堆的右孩子的NPL > 左孩子的NPL，则交换左右孩子。
4. 设置新堆的根节点的NPL = 右子堆NPL + 1

3、斜堆

斜堆也叫自适应堆，它是左倾堆的一个变种。和左倾堆一样，它通常也用于实现优先队列；作为一种自适应的左倾堆，它的合并操作的时间复杂度也是O(log n)。

它与左倾堆的差别是：

1. 斜堆的节点没有"零距离"这个属性，而左倾堆则有。
2. 斜堆的合并操作和左倾堆的合并操作算法不同。

斜堆的合并操作

1. 如果一个空斜堆与一个非空斜堆合并，返回非空斜堆。
2. 如果两个斜堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将"较小堆的根节点的右孩子"和"较大堆"进行合并。
3. 合并后，交换新堆根节点的左孩子和右孩子。

第 3 步是斜堆和左倾堆的合并操作差别的关键所在，如果是左倾堆，则合并后要比较左右孩子的零距离大小，若右孩子的零距离 > 左孩子的零距离，则交换左右孩子；最后，在设置根的零距离。

4、二项堆

二项堆是二项树的集合。在了解二项堆之前，先对二项树进行介绍。

1）二项树

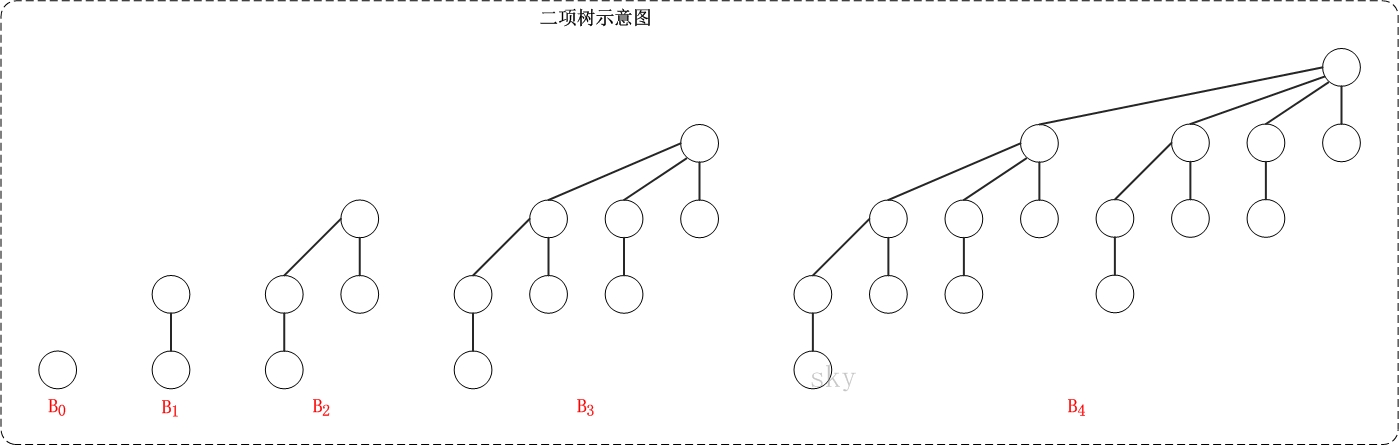
二项树是一种递归定义的有序树。它的递归定义如下：

1. 二项树B0只有一个结点；
2. 二项树Bk由两棵二项树B(k-1)组成的，其中一棵树是另一棵树根的最左孩子。

2）二项堆

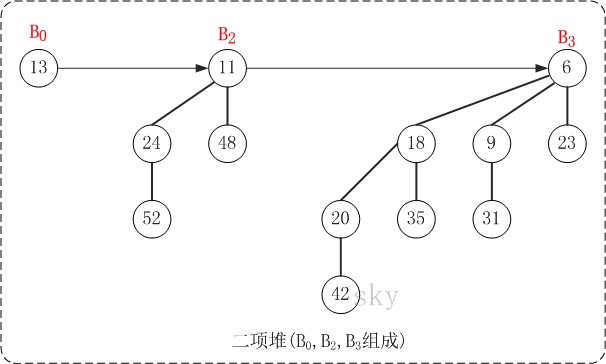
二项堆和之前所讲的堆(二叉堆、左倾堆、斜堆)一样，也是用于实现优先队列的。二项堆是指满足以下性质的二项树的集合：

1. 每棵二项树都满足最小堆性质。即，父节点的关键字 <= 它的孩子的关键字。
2. 不能有两棵或以上的二项树具有相同的度数(包括度数为0)。换句话说，具有度数k的二项树有0个或1个。

5、斐波那契堆

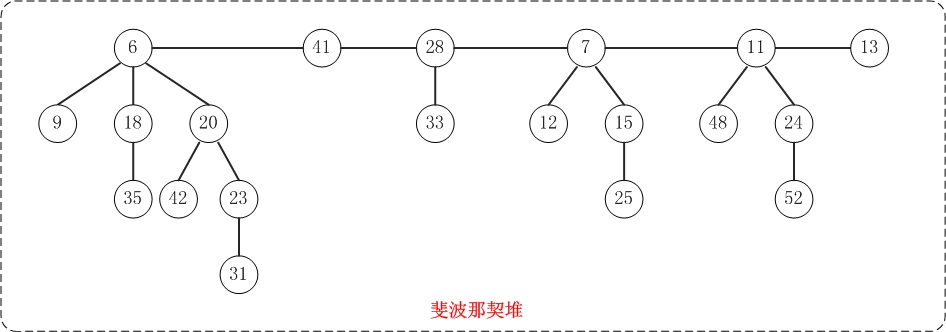
斐波那契堆(Fibonacci heap)是一种可合并堆，可用于实现合并优先队列。它比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O(1)。

与二项堆一样，它也是由一组堆最小有序树组成，并且是一种可合并堆。

与二项堆不同的是，斐波那契堆中的树不一定是二项树；而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的。

6、索引堆

索引堆是对堆进行了优化。

索引堆使用了一个新的int类型的数组，用于存放索引信息。

索引堆的交换操作交换的是元素的索引，而不是直接交换元素。

7、Treap 树堆

一棵treap是一棵修改了结点顺序的二叉查找树，如图，显示一个例子，通常树内的每个结点x都有一个关键字值key[x]，另外，还要为结点分配priority[x]，它是一个独立选取的随机数。

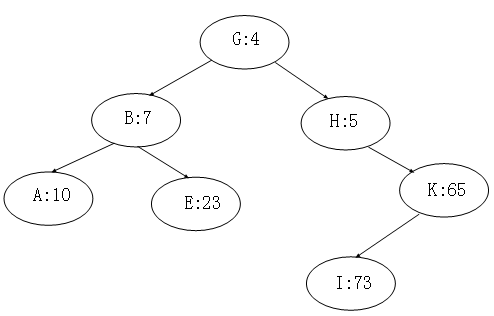
假设所有的优先级是不同的，所有的关键字也是不同的。treap的结点排列成让关键字遵循二叉查找树性质，并且优先级遵循最小堆顺序性质：

1. 如果v是u的左孩子，则key[v] < key[u].
2. 如果v是u的右孩子，则key[v] > key[u].
3. 如果v是u的孩子，则priority[u] > priority[u].

这两个性质的结合就是为什么这种树被称为“treap”的原因，因为它同时具有二叉查找树和堆的特征。